U(IS NOT, IS NOT)

You can compute anything at all using the negation of an AND gate (NAND) or an OR gate (NOR). I find that very interesting.

You can apply either of these simple rules recursively to compute anything:

• NAND: the result is 0 if both inputs are 1, otherwise it's 1
• NOR: the result is 1 if both inputs are 0, otherwise it's 0

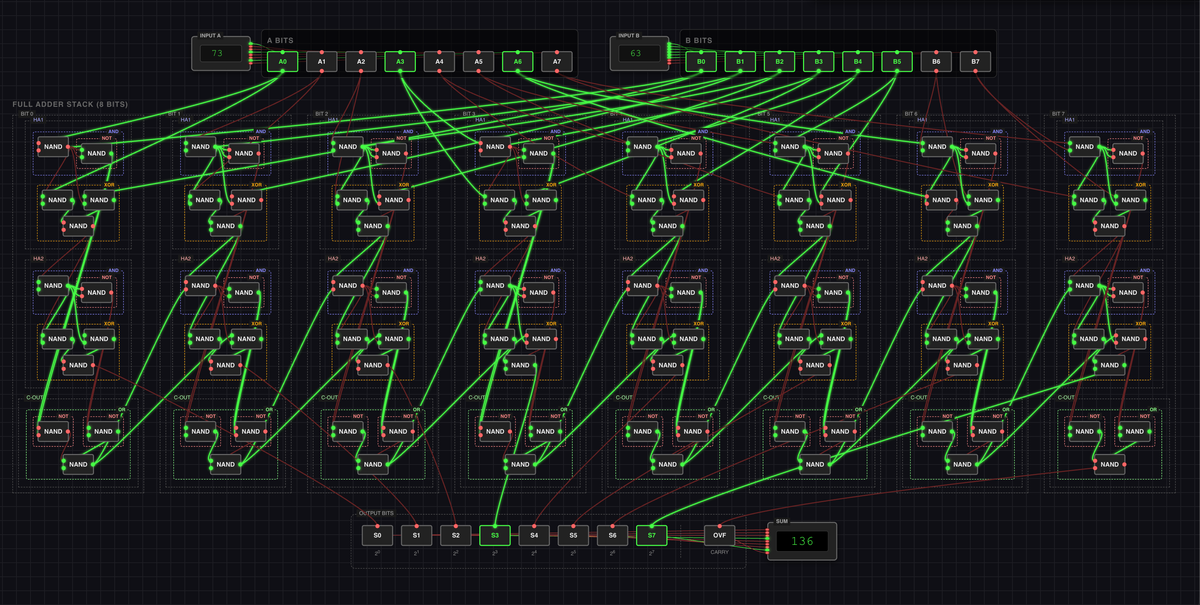
Here's an interactive program that adds two numbers using a series of NAND gates:

Adding Two Numbers Using NAND Gates

It’s possible to build any kind of digital logic using a single type of logic gate: either NAND gates, or NOR gates. A NAND gate takes two input bits (A and B) and produces one output bit according to this simple rule: 0 if both inputs are 1, otherwise 1

Made By NathanNathan Broadbent

It made me wonder if there might be any ontological implications (regarding the nature of existence and reality.)

John Wheeler’s "It from Bit" idea suggests that physical reality may even arise from binary distinctions.

John Archibald Wheeler Postulates “It from Bit” : History of Information

John Archibald Wheeler Postulates

Jeremy Norman’sHistoryofInformation.com Exploring the History of Information and Media through Timelines Search Site

If any kind of logic can emerge from just one rule, and a whole universe can be described by the evolution of a wavefunction, then it's interesting to think about the idea that "IS" and "IS NOT" could be somewhere at the very bottom. Not 0s and 1s, but "nothings" and "somethings".

Think of U(x,y) as the universe being a function of two inputs. (A giant, recursive, evolving, self-referential, maybe even self-fulfilling function.)

What if:

\( U^{(1)}(\text{IS NOT}, \text{IS NOT}) = \operatorname{NOR}(\text{IS NOT}, \text{IS NOT}) = \text{IS} \)