I'm writing a short story and one of the plot points involves Sagittarius A* (Sgr A*)—the supermassive black hole at the center of the Milky Way galaxy.

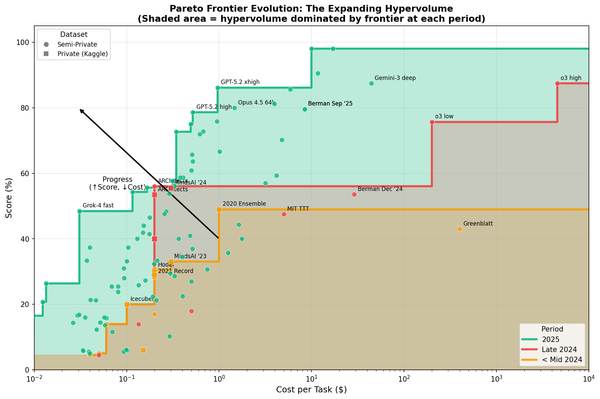
I wanted to read about Sagittarius A*, so I looked it up on Google. This is what I saw:

At first glance, this might not look too odd to you. But if you reread the first sentence...

"Sagittarius A* was the central supermassive black hole of the Milky Way galaxy."

was?

Now, you might not know much about cosmology, but one thing everyone should know is that black holes don't just suddenly disappear.

However...

Another thing you should know is that they do slowly disappear. Stephen Hawking predicted that black holes emit Hawking radiation, and if a black hole keeps emitting radiation then eventually it just withers away until it's completely gone.

So what's the expiration date of Sagittarius A*?

Approximately the year \(10^{87}\,\text{AD}\). One octovigintillion years from now.

1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 AD.

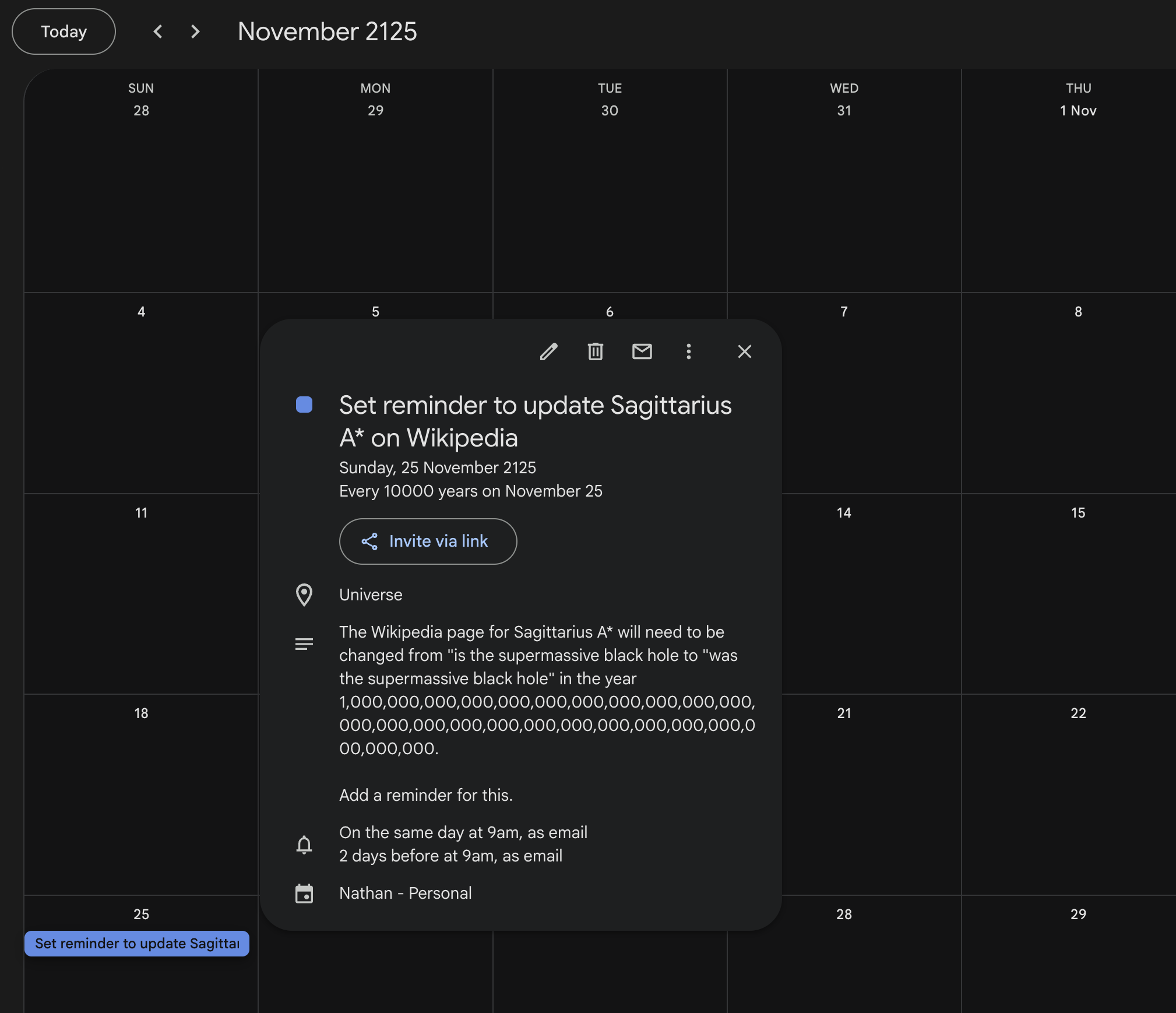
Imagine you're in the year \(10^{87}\,\text{AD}\). You've just logged in to Wikipedia, and you've decided that it's time to change "is the supermassive black hole" to "was the supermassive black hole".

So that's what was running through my mind for a split second. Have I just seen a Google search result from the year \(10^{87}\,\text{AD}\)? Is this some kind of glitch in the Matrix?

Anyway, there's a very mundane explanation for this error. Google's summary generation code picked one sentence from the fourth paragraph of the Wikipedia page:

Based on the mass and the precise radius limits obtained, astronomers concluded that Sagittarius A* was the central supermassive black hole of the Milky Way galaxy.

When you split that sentence in half and throw away "astronomers concluded that", you effectively yeet the black hole into the past tense. Or the reader into the distant future, for one mind-bending second.

Also I tried putting this on my Google Calendar, but you can only add events up to 100 years in the future.

How to Calculate the Death of a Black Hole

Sagittarius A* has a mass of about \(4.3 \times 10^6 M_\odot\), where \(M_\odot\) is the mass of the Sun.

For a neutral, non-rotating (Schwarzschild) black hole, the Hawking evaporation time is approximately:

\(t_{\text{evap}} \approx 2.14 \times 10^{67}\,\text{years} \times \left( \frac{M}{M_\odot} \right)^3\)

Plugging in \(M \approx 4.3 \times 10^6\,M_\odot\):

\(t_{\text{evap}} \approx 2.14 \times 10^{67} \times (4.3 \times 10^6)^3 \,\text{years}\)

Numerically this works out to \(t_{\text{evap}} \approx 1.7 \times 10^{87}\,\text{years}\)

But don't worry, that's nowhere close to the heat death of the universe. It will still take another \(10^{100}\) to \(10^{106}\) years for all matter and all black holes to disappear.

So we've got about ten quattuortrigintillion years left. That's about 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 years from now.

Then the universe will be a near-empty, cold expanse of a thin gas of photons and leptons. Sounds quite peaceful.

Oh... but actually we don't have that much time left. Stars that can host life are mostly done forming by around \(10^{12}\) to \(10^{14}\) years:

100,000,000,000,000 years.

After that, the universe is mostly dim embers, brown dwarfs, cooling white dwarfs, and very weak trickles of energy.

So we better get a move on. 100,000,000,000,000 years is not that much time when you think about it. And we have a lot to do.